Institut Charles Sadron TSP
Research
See below for details on selected topics:
(Polymer melt)(Topological interactions)(microtubules)(Self-assembled systems)(Glass-forming systems)
keywords of our research interest
Polymer physics
- solution and melts of flexible polymers
- long-range correlations in 3D polymers, e.g. corrections to chain ideality, viscoelastic hydrodynamic interactions
- two-dimensional polymer solutions and melts
- polymer films: conformation, dynamics, rheology
- topological constraints: polymer entanglements in thin films, melts of unconcatenated rings, energy storage by entanglements ("tanglotrons")
- living polymers
- semiflexible polymers and biofilaments (e.g. DNA, microtubules)
- polyelectrolytes: solutions, complexes, rheological properties of polymer jets
- mixed systems, e.g. colloidal stabilization by free polymer ("depletion stabilization"), mixtures of linear chains and star polymers
- more complex polymer architectures, e.g. hyperbranched polymers, transient and permanent polymer networks
- active systems, e.g. nanomotors connected to gels and energy storage, polymer fibers as a lever to convert energy into motion
Glass forming liquids and mechanical properties of amorphous solids
- glass-forming systems and disordered solids:
- glassy dynamics in supercooled polymer melts and films
- mechanical and viscoelastic properties of amorphous solids and networks
- voronoi tessellation and amorphous structures
Self-assembled systems
- micellization
- living polymerization
- associative polymers, telechelics, ionomers and transient networks
- mesophases in polymer systems: nematics, smectics, microphases
- chirality as a structure-forming factor, chiral recognition, spontaneous chirality
- chiral surfactant structures
- thermodynamics and conformation of block copolymers
- kinetics and morphology of self-assembling supramolecular nanostructures
- self-assembling systems stabilized by strong-interacting groups, organogelators
Systems inspired by biology
- amphiphilic and biomimetic heteropolymers
- biopolymers: peptides (beta-sheet structures, amyloids), DNA and its unconventional forms, polymorphic biofilaments (microtubules, actin)
- active systems: nanomotors, entanglements and energy storage, self-propulsion
Classical polymer solutions and melts have nonclassical long-range correlation effects
Together with S. Obukhov (Gainesville) we showed that the classical concept of chain ideality in polymer melts needs to be amended. In melts the screening of the excluded volume develops only gradually when the size of a chain segment increases. This leads to deviations from ideal chain conformations. In 3D the deviations are weak, but become more pronounced in spatial confinement (e.g. in thin films or in pores). Our work on these deviations from chain ideality are summarized in two comprehensive reviews [1,2].
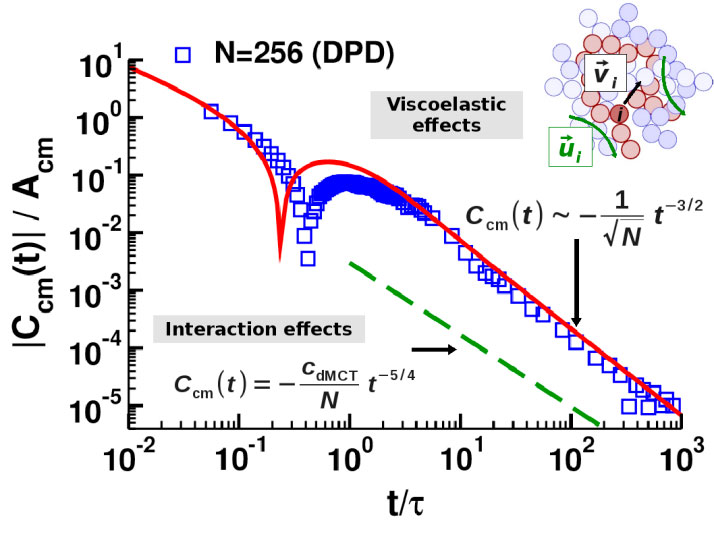
Figure 1. Velocity auto-correlation function Ccm (t) versus time t (both axes are scaled). The squares show the MD results for chains of length N=256 (and a polymer model where chains can cross each other). The lines show two theoretical results: The dashed line is the result, if excluded volume interactions are taken into account. The solid line is the VHI prediction implying a coupling of the chain conformation to the (transverse) collective velocity field in the melt (see inset). Figure adapted from [4].
It is natural to expect that the incomplete screening also affects the polymer dynamics, in particular the motion of the chain’s center of mass (CM). Contrary to the Rouse model, it is known empirically that there is an intermediate time interval where the CM moves subdiffusively. Subdiffusive motion can result from excluded volume interactions. We elaborated this effect [3,4], leading to an unexpected finding (cf. Figure 1): Excluded volume effects are too weak to explain the CM dynamics. Rather the subdiffusive CM motion is caused by “viscoelastic hydrodynamic interactions” (VHI), a novel effect implying that the screening of hydrodynamic interactions develops only gradually with time, as a consequence of the melt’s viscoelasticity. Thus, there is an intermediate time window where the effective viscosity of the melt is smaller than the steady-state viscosity. Our theory is in very good agreement with molecular dynamics (MD) simulations in 3D [4] and in 2D [5].
Long-range correlations in polymer systems were also studied as a possible means to stabilize colloidal suspensions. Empirically, it is known that a certain amount of free polymer in a colloidal suspension can enhance its stability. Yet, many basic features of this free-polymer induced (FPI) “depletion stabilization” are unknown. In collaboration with the experimental group of E. Bartsch (Freiburg) extensive theoretical studies of this stabilization were carried out (PhD thesis of A. Shvets) [6]. We found that the FPI interaction of two colloidal particles has a repulsive peak in semidilute polymer solution. The repulsion is most pronounced in theta solvents and is rooted in the excess ideal-gas free energy (i.e. lower entropy) of the chain ends confined in the “slit” between the colloidal particles. Yet, our analysis also shows that the FPI repulsion alone is not strong enough to yield sufficient stability for typical colloidal sizes of a few 100 nm. Some pre-stabilization, e.g. by an adsorbed (fluffy) polymer layer, is needed. We established that such a layer strongly enhances the depletion repulsion which can then stabilize colloidal suspensions.
[1] J. Wittmer et al., J. Stat. Phys. 2011, 145, 1017.
[2] A. N. Semenov, I. A. Nyrkova. In: Polymer Science: A Comprehensive Reference (Elsevier, Amsterdam, 2012), pp. 3-29.
[3] J. Wittmer et al., J. Chem. Phys. 2011, 134, 234901.
[4] J. Farago et al., Phys. Rev. Lett. 2011, 107, 178301; A. N. Semenov et al., J. Chem. Phys. 2012, 136, 244905.
[5] H. Meyer, A. N. Semenov, Phys. Rev. Lett. 2012, 109, 248304; A. N. Semenov, H. Meyer, Soft Matter 2013, 9, 4249.
[6] A. Shvets, A. N. Semenov, J. Chem. Phys. 2013, 139, 054905; A. N. Semenov, A. Shvets, Soft Matter 2015, 11, 8863.
Topological interactions: When they have an impact on polymer structure and their potential for applications
Chain connectivity implies another interaction: the “topological constraints” that the chains cannot cross each other. For (long) linear polymers in 3D melts, topological interactions affect the dynamics, but not the statics. The situation becomes different for ring polymers, since unconcatenated rings must remain unconcatenated and so effectively repel each other due to topological constraints. In collaboration with S. Obukhov we proposed that the conformation of a ring in a melt can be modeled as a collection of polydisperse Gaussian loops assembled in random trees, if the ring size is larger than the entanglement length (Ne ) [7]. This “decorated loop model” predicts that asymptotically long rings are compact, but the transition to compactness with increasing chain length N is very slow (cf. Figure 2). Compactness does not necessarily imply the surface of a polymer ring to be “smooth”; the surface can have a fractal surface dimension (d s ) different from the dimension (d) of space. Whether polymer rings have ds ? d or are marginally compact (i.e. ds ˜ d) is an open question. Our (ongoing) analysis of this point and of molten rings in general is inspired by the related problem of 2D polymer melts, which we extensively studied in the past (cf. [8] for a review).
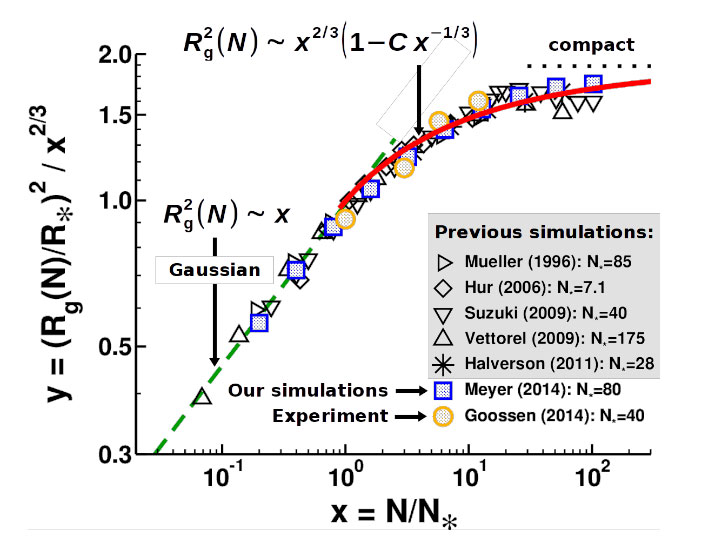
Figure 2. Radius of gyration R g versus N for unconcatenated ring polymers in a melt. The abscissa is scaled by N* ˜ N e and the ordinate such that compact behavior gives a horizontal line. Previous simulation results and experimental data are compared with our simulations. The solid line shows the prediction from the decorated loop model. Figure adapted from [7].
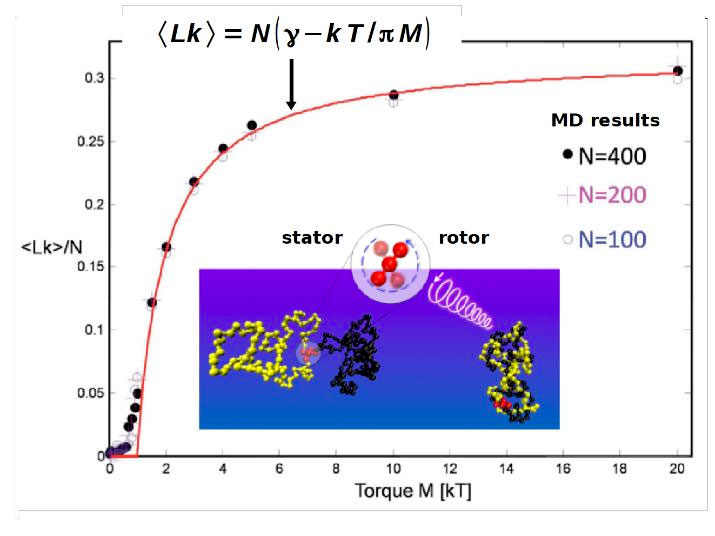
Figure 3.Main figure: Average interchain linking number Lk versus M for three chain lengths (symbols). The solid line shows the theoretical prediction with ? being the maximal entanglement density. Inset: Snapshots from the simulation showing the stator (brightened spheres) and rotor units (dark spheres) of the motor and the configurations of the separated polymer rings (left) and of the densely entangled rings (right). Figure adapted from [9].
Rings and topological interactions were also crucial in another project. Assume that two polymer rings are linked to the stator and rotor axes of a molecular motor (cf. Figure 3). Chain uncrossability implies that the rotation of the motor progressively winds up the rings and makes them collapse with increasing linking number Lk. This has two consequences [9]: i) Chain collapse leads to volume contraction, thereby converting rotational into translational motion. ii) The rotational energy of the motor can be stored as topological entanglements. We refer to such a device as a “tanglotron” [9]. By theory and MD simulations we established the relation between Lk and motor torque M of the tanglotron (cf. Figure 3) and also the associated free energy. We found that the free energy gain per entanglement is about 6 kT. The tanglotron is not just an academic curiosity. The SAMS group succeeded in inducing macroscopic contraction of a polymer gel by the integrated motion of light-driven molecular motors [10].
[8] N. Schulmann et al., Polym. Sci. Ser. C 2013, 55, 181.
[9] F. Weysser et al., Soft Matter 2015, 11, 732.
[10] Q. Li et al., Nat. Nanotechnol. 2015, 10, 161.
Beyond flexible linear chains: Examples from studies of polyelectrolytes and microtubules
Many polymers do not belong to the class of flexible linear chains. We worked on polymers with different architectures (e.g. hyperbranched polymers [11]), on semiflexible chains (e.g. microtubules, DNA) or on polyelectrolytes. Here we present some examples.
Polyelectrolytes (PEs). Usually PE solutions show a peak in the polyion/polyion structure factor for some value q* of the scattering vector q. The peak position q* reflects the PE/PE correlation length and depends on polymer concentration (c). In collaboration with the PECMAT group we studied the scaling of q* in a wide concentration regime and for PEs of varying intrinsic stiffness. In addition to two known scaling laws, namely q* ~ c1/2 for semidilute solutions and q* ~ c1/4 for fairly concentrated (weakly charged PE) solutions, we also found a new regime, where q* ~ c, if the concentration is above c ~ 1 mol/L and the PEs have intermediate stiffness [12]. We propose that this regime corresponds to a jammed regime with randomly oriented persistent segments, pre-empting the nematic transition. This may explain why fully developed nematic order is so difficult to observe in synthetic PEs (see also the PECMAT). The interplay of electrical charge and chain stiffness is also crucial for the behavior of PE complexes (PECs). In collaboration with A. Lazutin, and V. V. Vasilevskaya (Moscow) we analyzed by Monte Carlo simulations and analytical theory the structure of PECs consisting of two identical but oppositely charged macroions with varying stiffness [13]. We find two kinds of complexes, depending on chain stiffness. Stiff chains are organized into a “ladder” structure in which polymers are located parallel to each. As chain stiffness decreases, the energetically favored “ladder” conformation is transformed into a more disordered (entropically favorable) globular structure. The transition between globule and ladder conformations is driven by chain stiffness and gets sharper for longer chain lengths, likely becoming a thermodynamic transition in the large-N limit [13].
Microtubules (MTs). Microtubules have the form of a hollow cylinder resulting from the side-by-side association of linear (rod-like) protofilaments (PFs) which themselves are created by the head-to-tail polymerization of a “monomeric” building block, the tubulin dimer. If we disregard this internal structure and consider the cylinder as a semiflexible chain, the worm-like chain (WLC) model is expected to apply. However, this approach does not allow rationalizing some striking experimental observations, e.g. from motility assays where MTs are moved by kinesin motors on a surface (cf. Figure 4). Instead of only straight shapes, also arcs and rings are observed. In collaboration with H. Mohrbach (Metz) and F. Ziebert (Freiburg) we studied this unusual behavior. We proposed a model [14] taking into account the internal structure of the MT, which explains the unusual curved shapes and their formation [15]. The model builds on the following hypotheses: i) On the experimental time scale the tubulin dimer fluctuates between a straight state and an outward curved state [cf. Figure 4(a)]. The curved state has a lower (free) energy. ii) Nearest-neighbor interactions between the tubulin dimers along the PF favor the dimers to adopt the same state. The ground state of an isolated PF is thus curved. iii) Yet, in an MT the PFs are bound in a cylinder and the dimers cannot switch to the curved state without straining other parts along the perimeter of the MT. This strain gives rise to a bending energy, favoring the MT’s straight shape. These competing interactions allow rationalizing the curved shapes observed in motility assays [see Figure 4(b) and 4(c)] [15].
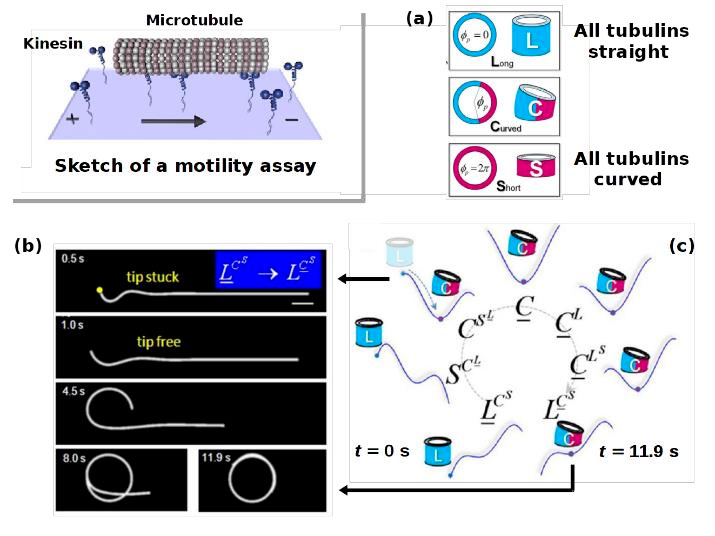
Figure 4. Inset in the upper left corner: Sketch of a motility assay. In the course of their motion the MTs can form arcs and circles. These shapes are unexpected from the WLC model, but can be understood from our “polymorphic” model. This model allows the tubulin dimer to adopt two states (straight and curved). Inclusion in the MT imposes constraints on the dimers so that a section of the MT can be either straight (all dimers straight or curved) or curved (only a portion of the dimers is curved) [panel (a)]. Implementing this model and accounting for the force exerted by the kinesin motors allows simulating the ring formation in a motility assay starting from an initially straight MT [panel (b)]. Panel (c) shows the sequence of states traversed (clockwise) in this ring formation. Panels (a), (b) and (c) are adapted from [15].
DNA. In collaboration with N.-K. Lee (Seoul) we studied conformational properties of DNA. Besides the standard right-handed B-form there are many other structures (triple stranded H-form [16], left-handed forms like the L-form and H-bond stabilized Z-form). The left-handed forms are not only fascinating; there is also increasing evidence for their biological role e.g. in the replication process. In this context, we study the B/Z-L transitions [17] under negative torsional stress. Another intriguing issue is how the protein ADAR1 turns B-DNA into Z- DNA. Combining our theoretical ideas with FRET and CD experiments in Prof. Hong's group (Seoul) we have recently obtained the affinities of ADAR1 to the B-form and Z-form. The measured affinity of ADAR1 to the B-form is found to be much smaller than that to the Z-form, but still remains significant.
[11] P. Polinska et al., Eur. Phys. J. E 2014, 37, 12.
[12] P. Lorchat et al., EPL 2014, 106, 28003.
[13] A. A. Lazutin et al., Macromol. Theory Simul. 2012, 21, 328.
[14] H. Mohrbach et al., Eur. Biophys. J. Biophys. Lett. 2012, 41, 217; H. Mohrbach, I. M. Kulic, Phys. Rev. E 2012, 85, 031903.
[15] F. Ziebert et al., Phys. Rev. Lett. 2015, 114, 148101.
[16] I. B. Lee et al., Biophys. J. 2012, 103, 2492; N.-K. Lee et al., Eur. Phys. J. E 2013, 36, 57.
[17] A.-Y. Kwon et al., Phys. Rev. E 2016, 93, 022411.
Self-assembled systems
In the context of self-assembled systems, we worked on several problems [18-21], also in collaboration with colleagues from the ICS [20] and outside [21]. Here we will describe some aspects of this work.
Living polymers. Living polymers have reversible bonds that can break and recombine. We studied the kinetics of this self-assembly process based upon an open associating mechanism and assuming that unimer attachment/detachment at a chain end is the elementary kinetic step. In spite of much past effort an analytical solution for the kinetics of the chain length distribution (CLD) was unknown. This gap is filled in [18]. We determined the CLD after a temperature (T) jump for different cases, including weak and strong T-jumps, and gave a comprehensive description of the associated relaxation process. Complementary to Ref. [18] is the study of Ref. [19] that considers theoretically the thermodynamic and correlation properties of equilibrium living polymers where the scission and recombination of any bond is allowed. Three cases are treated: i) living polymers where ring formation is forbidden, ii) classical living polymers with ring formation (like in liquid sulfur), and iii) directional living polymers with rings. Here “directional’’ means that the chemical structure of the chain defines an arrow along the chain. By virtue of the polymer-magnet analogy a mapping on the n-vector model is achieved. This mapping reveals that the three cases fall in different universality classes: case i) corresponds to n=0 (self-avoiding walk), case ii) to n=1 (Ising model), and case iii) to n=2 (XY- model). An essential part of the new results concerns spatial correlation functions, e.g. Gp(r) for the total polymer concentration. For large distances r major qualitative differences are found for Gp(r) in the three cases. These differences have implications for FPI interactions e.g. in colloidal suspensions, cf. [6].
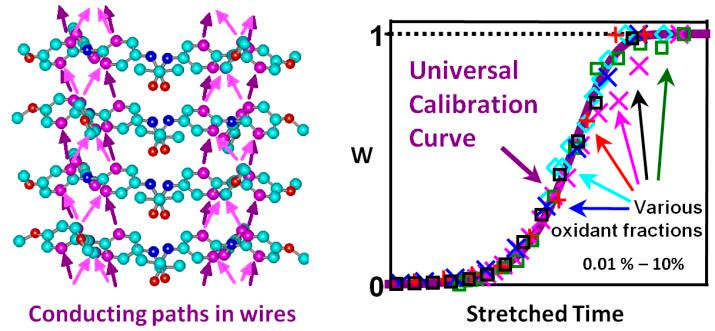
Figure 5. When exposed to light or oxidants triarylamines in chloroform self-assemble into conducting nanowires (cf. left panel for paths of electron transport). This fibrillization is autocatalytic: Initially, bicolumnar fibrils with defects are formed by a nucleation- growth process, leading to a weak increase of the weight fraction (w) of aggregated amines (right panel). w rapidly increases when the fibrils self-replicate by scission at the defects and recombi- nation. The theoretical master curve for w versus time agrees with experimental data (right panel). Figure taken from [20].
Supramolecular conducting nanowires. We closely collaborated (and still do) with Dr. Nyrkova (post-doc) and experimental groups, in particular with the SAMS group , on the self-assembly of supramolecular triarylamine based nanowires (STANWs). We elucidated the physical properties of the STANWs, their packed structure and the kinetics of the associated radical-controlled supramolecular polymerization by multi-scale modeling and various experimental tools [20]. The aggregation of the triarylamine (TAA) units in chloroform can be triggered by light or oxidants. Our all-atom computer modeling revealed the two-columnar “snowflake” internal structure of the fibers involving p-stacking of TAA with alternating handedness, in agreement with AFM and small-angle X-ray data. The polymerization process and the kinetics of the formation and decay of the triaryl-ammonium radicals were studied by various experimental techniques. Our modeling reproduces and explains these experimental data: It shows that the supramolecular self-assembly starts by the production of radicals that are required for the nucleation of double-columnar fibrils followed by their growth in double-stranded filaments. We also elucidated the kinetics of this self-assembly process being characterized by a complex self-replicating behavior (cf. Figure 5).
Self-assembly of colloidal superstructures. Consider dipolar magnetic colloidal particles placed in an external time-dependent magnetic field. Assume the field to vary on a time scale long relative to the dipolar relaxation time, but short relative to the time for particle motion. Then, the magnetization can equilibrate before the field changes, whereas the particle motion feels the time-averaged interaction created by the field. In collaboration with M. Kulic (Frankfurt) we studied this effective interaction. The interaction comprises many-body terms and has interesting properties [21]. For instance, the three-body term is of the same order of magnitude as the two-body term, scaling with distance in a van-der-Waals-like fashion (~1/r6 ). However, contrary to the isotropic two-body term the three-body term is anisotropic, favoring chain-like structure. This can explain the emergence of colloidal chains found experimentally when the particle number is not too large. The theory also rationalizes why chains aggregate into membranes when the particle number is large [21]. The effective interaction between two membranes may be attractive or repulsive, depending on the mutual orientation of the membranes. This can explain why hollow foam-like structures have been observed experimentally in fairly dense colloidal suspensions.
[18] A. N. Semenov, I. A. Nyrkova, J. Chem. Phys. 2011, 134, 114902.
[19] A. N. Semenov, Soft Matter 2014, 10, 9534.
[20] I. A. Nyrkova et al., ACS Nano 2014, 8, 10111.
[21] I. M. Kulic, M. L. Kulic, Phys. Rev. Lett. 2013, 111, 198301.
Glass-forming systems and disordered solids
In the past years we studied properties of disordered solids (glasses, networks) and of the liquid state above the glass transition temperature Tg . Our work involved various aspects: the dynamics of super-cooled polymer melts [22,23], the thermodynamics, structure and dynamics of the “Voronoi liquid” [23], the thermodynamic nature of vitrification in a (1D) spin-glass model [24], the linear mechanical response of glass-forming liquids and networks [25,26], and the uniaxial deformation of polymer glasses and the nano-indentation in glassy polymer films [27]. The latter work was carried out with the PMTP group (thesis of M. Solar). Some of these results will be briefly discussed here.
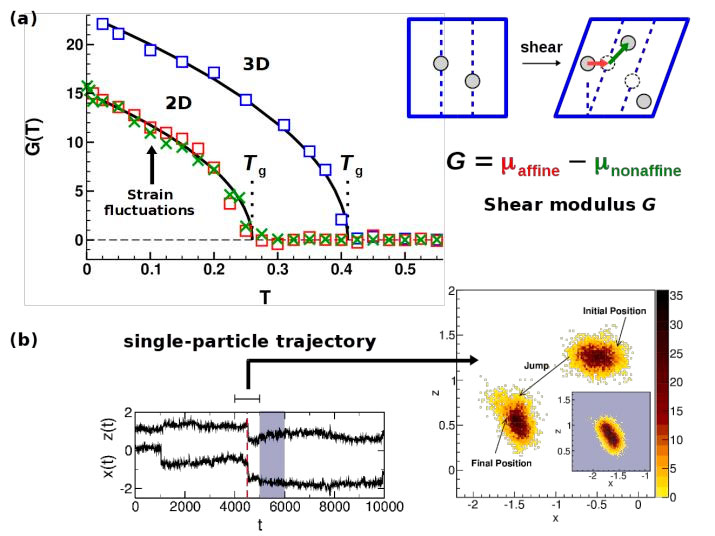
Figure 6. Panel (a): Shear modulus G versus T from simulations of simple glass-forming liquids in 2D and in 3D. In the liquid (T > Tg ) G vanishes, but is finite in the glass. For the 2D system two ways to calculate G are compared: the strain fluctuation method (crosses) and the “stress-fluctuation” method (squares). The latter expresses G as the difference of two terms related to affine and nonaffine displacements (shown by the red and green arrows in the upper sketch). Figure adapted from [25]. Panel (b): Analysis of a single-particle trajectory in a supercooled polymer melt. Long periods of monomer localization interrupted by short, jump-like transition can clearly be identified. Figure adapted from [22].
Mechanical properties of glasses/amorphous solids. The difference between a liquid and a solid manifests itself in the response to a weak shear deformation. The liquid flows, whereas the solid has an elastic response, the strength of which is quantified by the magnitude of the shear modulus G. In collaboration with H. Xu (Metz) we studied different methods to determine G for glasses for simple glass-forming liquids and for elastic networks [25,26]. One method employs the fluctuations of the strain, the other the fluctuations of the stress. Both give the same T dependence for G [cf. Figure 6(a)]. In addition, our work gives an interpretation of the stress fluctuation method which expresses G as the difference of an affine and a nonaffine part [cf. Figure 6(a)]. One can show that these parts are related to the rules of how to transform fluctuations between ensembles of thermodynamically conjugate variables (here stress and strain) [25].
Liquid state above T g. On cooling toward low T the slowing down of the relaxation is accompanied by an interesting behavior of the trajectories of individual particles [cf. Figure 6(b)]: Long periods where a particle fluctuates around a temporary “equilibrium” position (solid-like behavior) are punctuated by a jump-like motion to a new position where it is localized again [22]. These dynamic anomalies develop without pronounced changes of standard static correlation functions, which do not lend themselves to correlate the slowing down of the relaxation with the growth of a static length scale. From a theoretical point of view such a correlation is attractive and the search for it is an active line of research in glass physics. In this context, we pursued two ideas: i) Recent studies on structural glasses often draw upon analogies with spin glasses. We propose a new spin-glass model without quenched disorder as a coarse-grained model for structural glass formers [24]. The model exhibits a sharp freezing transition of thermo-dynamic origin, accompanied by a growing static length scale. ii) If the static structure factor does not carry information about a growing length scale, perhaps higher-order correlation functions do. One idea was to consider the Voronoi tessellation of a liquid because the Voronoi cell is defined by a particle and all of its neighbors, and so a multi-point correlation. Although this search for a growing length scale when applied to a glass-forming polymer melt was not successful [23], our study still uncovered a new quantity: the “geometric polarization” given as the vector between the particle and the center of gravity of the Voronoi cell. This polarization is akin to a force and so allows defining a novel type of simple liquid, the “Voronoi liquid” [28], whose behavior is currently studied (thesis of C. Ruscher).
[22] J. Helfferich et al., Phys. Rev. E 2014, 89, 042603; ibid, 042604.
[23] J. Farago et al., Eur. Phys. J. E 2014, 37, 46.
[24] A. N. Semenov, J. Chem. Phys. 2015, 143, 044510.
[25] J. Wittmer et al., J. Chem. Phys. 2013, 138, 12A533.
[26] D. Li et al., J. Phys.-Condes. Matter 2016, 28, 045101.
[27] M. Solar et al., Phys. Rev. E 2012, 85, 021808 ; Eur. Phys. J. E 2013, 36, 29.
[28] C. Ruscher et al., EPL 2015, 112, 66003.